BASAMAK KORELASYON AĞI TANIMI
Önceki yazıda basamak korelasyon ağının hangi problemlerin çözümü için ortaya çıktığı anlatılmıştır. Bundan dolayı, basamak korelasyon iki anahtar fikri birleştirir; ilki basamak mimarisi ki burada bahsi geçen gizli birimler ağa bir kez eklenir ve eklendiği zamanda değişmezler. İkinci önemli durum ise, öğrenme algoritmasıdır. Bu algoritma yeni gizli birimler yaratır ve yükler. Burada aslında yapılmak istenen şey her bir gizli birim için, yeni birimlerin çıkışı ile elimine edilmeye çalışılan artık hata sinyal değerinin korelasyon büyüklüğünü maksimize etmektir.
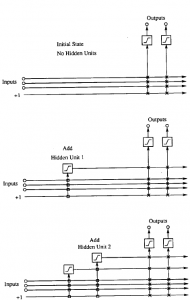
Basamak mimarisi Şekil 1 de görüldüğü üzere ilk önce bazı girişler ile bir veya daha fazla çıkışlar ile başlar ki bu arada gizli birimler yoktur. Giriş ve çıkış sayıları problem tarafından verilir. Her bir giriş her bir çıkış değerine ayarlanabilir bir ağırlık ile bağlıdır. Ve tabi ki bias girişi +1’e göre kalıcı olarak ayarlanır. Çıkış birimleri ağırlıklandırılmış girişlerin doğrusal olarak toplamını üretebilir veya doğrusal olmayan aktivasyon fonksiyonu çalıştırabilir.
Gizli birimler ağa teker teker eklenir. Her bir yeni gizli birim ağın her bir orijinal girişlerinden ve daha önceki gizli birimlerden bağlantı alır. Gizli birimlerin giriş ağırlıkları net’e eklendiği zaman donar; sadece çıkış bağlantılar tekrarlı olarak eğitilir. İçerdeki bazı ağırlıklar sıfır olmadıkça, her bir birim bu nedenle ağa yeni bir ‘katman’ ekler. Bu durum çok güçlü bir yüksek seviye özellik sezinleyicinin yaratılmasına olanak sağlar; ayrıca derin yapılara ve gizli birimlere yüksek giriş yelpazesi sağlar. Yeni birimler eklendikçe yapının (ağın) derinliği ve giriş yelpazesinin minimize edilmesine yönelik bazı stratejiler mevcuttur. Fahlman ve Lebiere bunun üzerine bazı çalışmalar yapmıştır.
Şekil 1 Basamak mimarisi (başlangıçtaki hali ve sonradan gizli birimlerin eklenmesini göstermektedir. Dik çizgiler içerideki tüm aktivasyon toplamını gösteriyor. Kutu bağlantılar ise donmuş halde olanlar, X bağlantılar ise tekrarlı eğitimlerdir) (Fahlman ve Lebiere, 1990)