Basamak Korelasyon Sinir Ağı-Bölüm 4- Derin Öğrenme

Genetik Basamak Korelasyon Öğrenme Algoritması

Genetik algoritmalar, doğal seçim ilkelerine dayanan bir arama ve optimizasyon yöntemidir. Temel ilkeleri John Holland (1975) tarafından ortaya atılmıştır. Geleneksel optimizasyon yöntemlerine göre farklılıkları olan genetik algoritmalar, parametre kümesini değil kodlanmış biçimlerini kullanırlar. Olasılık kurallarına göre çalışan genetik algoritmalar, yalnızca amaç fonksiyonuna gereksinim duyar. Çözüm uzayının tamamını değil belirli bir kısmını tararlar. Böylece, etkin arama yaparak çok daha kısa bir sürede çözüme ulaşırlar (Goldberg, 1989). Diğer bir önemli üstünlükleri ise çözümlerden oluşan populasyonu eş zamanlı incelemeleri ve böylelikle lokal en iyi çözümlere takılmamalarıdır (Emel ve Taşkın, 2002).

Quickprop algoritması yerine kullanılan genetik algoritması da geri yayılımlı algoritmaya karşın bazı avantajları mevcuttur. Özellikle, bu iki algoritmada lokal minimuma yakınsama olasılığını azaltmayı ve gradyan bilgisi olmamasına karşın uygulamayı desteklemeyi içerir. Fahlman gradyan inişi potansiyel problemde lokal minimum çözümü yakınsamasında korelasyonda basamak korelasyonu aday birimlerin olduğu popülasyonun eğitiminde en fazla ilişkili olanı seçer ve ağa onu ekler ve bunun için küçük bir popülasyon-4 ila 8 birim- kullanırken hiçbirinin birbirleriyle iletişime geçmemesini sağlar. Genetik algoritmalar genellikle çok daha büyük nüfusları korur ve çapraz rekombinasyon operatörü aracılığıyla bireylerin etkileşimini kullanır (Potter, 1992).

Genetik algoritmalar ile sinir ağlarını eğitmek için çeşitli başarılar elde edilmiştir. Montana ve Davis sonar veri analizi alanında dizi karakterizasyonunu yapmak için genetik algoritma kullanımı ile bir sinir ağı eğitmiştir (Montana ve Davis, 1989). Yaptıkları çalışma ile genetik algoritma geri yayılıma nazaran daha iyi sonuçlar vermiştir. Ek olarak, Whitley ve Hanson bazı klasik ileri beslemeli test olgularını çözmek için ki bunlar exclusive-or problemi, 424-encoder, ve two-bit adder, genetik algoritmaları kullanarak sinir ağlarını eğitmişlerdir (Whitley ve Hanson 1989). Ayrıca, Whitley ve arkadaşlarının tespitine göre geleneksel genetik algoritmalar daha büyük ağlara uygulandığı zaman, kabul edilebilir bir çözüm ağırlık bağlantısını bulmakta sık sık hata vermektedir (Whitley vd. 1989, 1990, ve 1991)

5.11. Basamak Korelasyon Sinir Ağlarını Budama

Basamak korelasyon mimari uyarlaması uygulamanın ağ topolojisine uyar, fakat nöronlar boyunca sabit bir bağlantı şeması kullanır. Bu şema her bir durum için geçerli olmayabilir. Bu problemi yenmek için ağ çıkışında en az etkisi olan bağlantılar bulunur ve çıkartılırlar. Daha az bağlantı ağın genelleştirme yeterliliğini ve öğrenme hızını geliştirebilir, eğer ilgilenilmezse bu ağın yaklaşım gücünü de azaltabilir. Thivierge ve arkadaşları (2003) BKSA’nın en az önem niteliği taşıyan bağlantılarını budamak için optimum beyin hasarı (optimal brain damage (OBD)) metodunu kullanmışlardır. OBD tekniği her bir bağlantı için çıkıntı değerlerini ki bu ağ çıkışında bağlantının etkisini ölçer, hesaplar. Bu değer hata fonksiyonunun ikinci dereceden Taylor tahminini ihmal ederek hesaplanır. Ortalama karesel hata kullanımı denklemi aşağıdaki hale getirir,

(1)

Burada O çıkış nöronların kümesini, yo ise o nöronunun çıkışını, ts;o nöron o ve örnek s için istenen çıkışı ve s(w) bağlantının w ağırlığına bağlı çıkıntı değerini gösterir. Sonrasında daha az çıkıntı değerleri olan bağlantılar budanabilir. BKSA’larında OBD tekniği hem aday eğitiminin sonunda giriş bağlantılarını budamak için hem de eğitim adımının sonunda çıkış bağlantılarını budamak için kullanılır (Thivierge vd, 2003). Thivierge ve arkadaşları sınıflandırma problemleri üzerinde bu yöntemi test etmişler ve OBD tekniği bağlantıların yarısını kaldırmış ve genelleştirme yeteneği görülmemiş örnekler üzerinde geliştirilmiştir (Bal´azs, 2009).

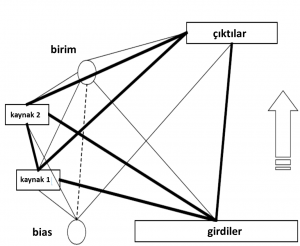
Bilgi Tabanlı ve Kural Tabanlı Basamak Korelasyon Ağı

Birçok uygulamada büyük miktarda problem hakkında öncül bilgi mevcuttur. Tamamıyla yeni bir yaklaşım kurmak yerine mevcut bilgiyi daha hızlı ve daha iyi bir sonuç almak için kullanmak cazip gelmektedir. Schultz ve Rivest (2001) tarafından yayımlanan çalışma bilgi tabanlı basamak korelasyon (BTBK) sinir ağlarını işaret etmektedir (Şekil 1). BTBK ağları tek aday birimler olarak önceden eğitilmiş modülleri kullanır ve eğer çözüm için onlar istenirse ağın içine inşa eder. Bu modüller, iç içe ağlar gibi hareket eder, birçok giriş bağlantılarını birleştirir ve basamak korelasyon ağının sahip olduğu gibi bir çok çıkış sağlar. Tek şart bu modüllerin türevi eğitim süreci için hesaplanır olmasıdır. BTBK birçok oyuncak ve gerçekçi örnekler üzerinde test edilmiştir. Bu örnekler çeşitli geometrik biçimler, sesli harf tanımı ve gen ekleme tayini içermekte olup önemli ölçüde çoklu görev öğrenme metodları üstün olmuştur (Schultz ve Rivest, 2001). Aynı zamanda bu örnekler üzerinden bilgi tabanlı yapay sinir ağları (BTYSA) algoritmaları da kullanılmış ve iyi sonuçlar elde edilmiştir (Schultz vd, 2006).

BTBK’nın en büyük limitlerinden birisi eğer kompleks modüller kullanılmışsa, hesaplama olarak pahalı olabilir. Diğer bir ciddi sorun ise BTBK genellikle tek aday nöronlar yerine bu kompleks modülleri seçer, çünkü bir tek eğitim adımı altında sonuçlar daha doğru olabilir. Her zaman yararlı olmayabilir ve gelecek araştırmalara ışık tutmak namına aday modüllerin komleksitesi cezalandırılmalıdır.

Kural tabanlı basamak korelasyon (KTBK) sinir ağları Thivierge ve arkadaşları (2004) tarafından BTBK’nın bir çeşidi olarak yayımlanmıştır. KTBK ağları kural tabanlı ağlar oluşturmak için kural tabanlı öncelikli bilgiyi kullanır. Bunlar sadece ‘OR’ ve ‘AND’ kurallarını yaratan kural tabanlı yapay sinir ağları (KTYSA)’nın genelleştirilmiş hali olarak düşünülebilir. KTBK ağları herhangi m-n kuralı yaratabilir (m notasyonu n’lerin arasında seçilen özellik sayısıdır. KTBK, gen ekleme tayini problemi üzerinde KTYSA, BK ve BTBK’dan daha iyi sonuçlar göstermiş olup (Schultz, 2007), henüz kapsamlı bir karşılaştırma yayımına rastlanılmamaktadır (Bal´azs, 2009).

Şekil 1 BTBK Ağı (varsayımsal olarak iki tane kaynak ağ ve bir sigmoid ağ içerir. Kesikli çizgiler tek bir bağlantı ağırlığını, ince çizgiler ağırlık vektörlerini ve kalın çizgiler ise ağırlık matrislerini temsil eder. Ok ise aktivasyon akış yönünü gösterir) (Schultz vd, 2006)