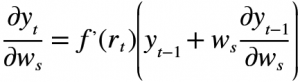Basamak Korelasyon Sinir Ağları Türleri-Bölüm3

Tekrarlı Basamak Korelasyon Sinir Ağları

Eğer örneklerin sırası belirli bir modelse, rekurrent (tekrarlı) sinir ağları (RSA) ileri beslemelerden daha iyi probleme uyumlu olabilir. RSA güncel olan veya önceki katmanlara doğru geri beslemeli bağlantılara sahiptir, böylece veri ağ içerisinde yayılabilir. Bu verileri kullanarak giriş ve çıkış modellerinin tanıma yetisi kısa bir zaman diliminde simule edilebilir. Ne yazık ki genel bir RSA için etkili bir öğrenme algoritması bulunmamaktadır. Fahlman (1991) tarafından yayımlanan makalesinde belirtildiği üzere, sadece bazı rekurrent mimari öğrenme metodları rekurrent basamak korelasyon mimarisinin de içinde yer aldığı etkili öğrenme metodlarına sahiptir (Fahlman, 1991). Çünkü Basamak korelasyon sinir ağı (BKSA) eğitimi dondurulan bir nöronun ağırlıkları değişmez, yeni aday nöronlar aktif nöronlara doğru bağlantılara geri besleme yapamazlar. Böylece tek seçenek, Rekurrent Basamak Korelasyon (RBK) tarafından uygulanan mimari, her bir nöron kendi-rekurrent (tekrarlı) bağlantısına (kendi çıkışı bir giriş değeri gibi davranır) sahip olduğu zaman ki bu aday öğrenme süresince eğitilebilir ve sonrasında dondurulur. Sonrasında nöronların hesaplama modeli şöyle değişir:

                                                               (1)

y_t-1, y_t sırasıyla t-1 ve t zamanlarındaki çıkışları, x_t,k t zamanında k’nıncı bağlantının girişini, w_k k’nıncı ileri besleme bağlantısından bir başka nörondan gelen geçerli ağırlığı, w_s kendi-rekurrent bağlantısının ağırlığını ve f ise aktivasyon fonksiyonunu göstermektedir. Aday eğitim süreci boyunca takip eden türevler kullanılır,

                                                                      (2)

 

                                                                      (3)

Burada, 1≤ i ≤n ve f ^, ise r girişine göre aktivasyon fonksiyonunun türevidir. y_t-1 ‘in türevi ve y_t-1 ‘in çıkış değeri önceki öğrenme adımından elde edilebilir. Kolay görülebileceği üzere RBK mimarisi KSBK değişkeni ki bu ağın derinliğini sıkıştırma kabiliyetine sahip, ile birleştirilebilir. Şekil 2 bu duruma örnek gösterilir.

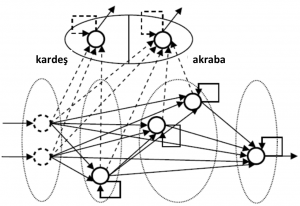
Şekil 2 RBK ile KSBK kombinasyonu (Bal´azs, 2009)

Kesikli bağlantılar kendi-rekurrent çevriminin de içinde bulunduğu eğitimlerdir. Bu yapı mantıklı görülebilir fakat henüz bu kombinasyonun yer aldığı ampirik çalışmalar bulunmamaktadır (Bal´azs, 2009).

Gelişen Basamak Sinir Ağları (GBSA)

Bir basamak ağ mimarisi tanımlanacak olursa, nöronların içeriği, p, giriş nöron sayısı, bir katmandan diğerine artmaktadır. İlk katmanda, nöron iki girişe bağlıdır, x_i1, …, x_i2, i₁ ≠ i₂ є (1, m). Giriş x_i1 minimal hatayı sağlayan tek girişli nöronu temsil etmektedir. İkinci katmanda, yeni nöron x_i1 girişine ve ayrıca bir önceki nöronun çıkışına bağlıdır. Bu nöronun üçüncü girişi ise çıkış hatasında maksimum bir düşüş sağlayan girişe bağlanabilir. Yeni katmandaki her bir nöron aynı yolla bağlanabilir.

Daha biçimsel olarak, r’ninci katmandaki nöron p = r + 1 girişe sahiptir. Lojistik aktivasyon fonksiyonu için, bu nöronun çıkışı olan z_r aşağıdaki gibi yazılabilir,

                                                                    (4)

r katman sayısını,  u = (u₁,…, u_p) r’ninci nöronun px1 giriş vektörüdür.

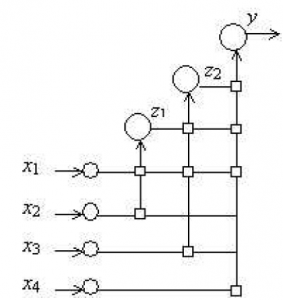
Örnek olarak Şekil 3 m=4 girişli ve r=3 katmanlı bir basamak ağını gösterir. Şekil 3’te tasvir edilen kareler sinaptik bağlantılarla beraber çıkış nöronu, z₁ ve z₂ çıkışlarıyla iki gizli nöron ve x₁…x₄ girişlerini göstermektedir.

Şekil 3 Üç Katmanlı Eğitilmiş Basamak Ağı (Schetinin, 2005)

Böylece, yukarıda bahsedilen algoritmanın kullanımı, önceki özelliklerle birlikte katılan her özellik için çıkış hatasını azaltmak için bir ad hoc tutumu tahmin edilebilir. Bu çıkış hatası bir validasyon (doğrulama) veri kümesi ile değerlendirilir ise, alakasız gibi gereksiz özellikler sonuçtaki ağda müdahil olmaya olası olduğunu varsaymak doğaldır.

Düzenlilik kriteri, C_r, r’ninci nöron için görülmemiş örnekler ki bunlar nöronun sinaptik ağırlıkların uydurulması için kullanılmamıştır, üzerinde hesaplanır. Bu bağlamda C_r değerleri verilen bağlantılarla nöronun genelleştirilme kabiliyetine bağladır (C_r değeri sınıflandırılamamış validasyon (doğrulama) örneklerinin sayısına orantılı olarak artar). Diğer bir anlamda, r’ninci nöron alakasız bağlantılar ile tüm görülmemiş örnekleri doğru bir şekilde sınıflandıramayabilir ve bu yüzden C_r değeri yüksek olması beklenir. Bu algoritmanın arkasındaki fikir, ilgili bağlantıları ile nöronların seçmek için yukarıda bahsi geçen kriteri kullanmaktır. Bu kriter şunu belirtir; eğer r’ninci nöron için hesaplanan C_r değeri önceki nöronda hesaplanan C_r-1 ‘den küçük ise, r’ninci nöron bağlantısı önceki katmandan daha uygundur, aksi halde onlar daha az uygundur. Eğer bu kural karşılanırsa, r’ninci nöronun ağırlıkları ve bağlantıları ağa eklenir. Verilen başarısız girişimler sonrasında bu kurala istinaden hiçbir nöron kabul edilmezse, algoritma durur ve r’ninci nöron minimum C_r değeri ile çıkış nöronu olarak kabul edilir (Schetinin, 2005).