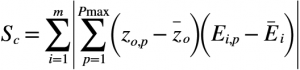Basamak Korelasyon Sinir Ağları Türleri- Bölüm 2- Derin Öğrenme

BASAMAK KORELASYON AĞI TANIMI

Önceki yazıda basamak korelasyon ağının hangi problemlerin çözümü için ortaya çıktığı anlatılmıştır. Bundan dolayı, basamak korelasyon iki anahtar fikri birleştirir; ilki basamak mimarisi ki burada bahsi geçen gizli birimler ağa bir kez eklenir ve eklendiği zamanda değişmezler. İkinci önemli durum ise, öğrenme algoritmasıdır. Bu algoritma yeni gizli birimler yaratır ve yükler. Burada aslında yapılmak istenen şey her bir gizli birim için, yeni birimlerin çıkışı ile elimine edilmeye çalışılan artık hata sinyal değerinin korelasyon büyüklüğünü maksimize etmektir.

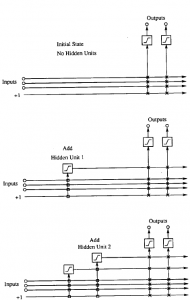
Basamak mimarisi Şekil 1 de görüldüğü üzere ilk önce bazı girişler ile bir veya daha fazla çıkışlar ile başlar ki bu arada gizli birimler yoktur. Giriş ve çıkış sayıları problem tarafından verilir. Her bir giriş her bir çıkış değerine ayarlanabilir bir ağırlık ile bağlıdır. Ve tabi ki bias girişi +1’e göre kalıcı olarak ayarlanır. Çıkış birimleri ağırlıklandırılmış girişlerin doğrusal olarak toplamını üretebilir veya doğrusal olmayan aktivasyon fonksiyonu çalıştırabilir.

Gizli birimler ağa teker teker eklenir. Her bir yeni gizli birim ağın her bir orijinal girişlerinden ve daha önceki gizli birimlerden bağlantı alır. Gizli birimlerin giriş ağırlıkları net’e eklendiği zaman donar; sadece çıkış bağlantılar tekrarlı olarak eğitilir. İçerdeki bazı ağırlıklar sıfır olmadıkça, her bir birim bu nedenle ağa yeni bir ‘katman’ ekler. Bu durum çok güçlü bir yüksek seviye özellik sezinleyicinin yaratılmasına olanak sağlar; ayrıca derin yapılara ve gizli birimlere yüksek giriş yelpazesi sağlar. Yeni birimler eklendikçe yapının (ağın) derinliği ve giriş yelpazesinin minimize edilmesine yönelik bazı stratejiler mevcuttur. Fahlman ve Lebiere bunun üzerine bazı çalışmalar yapmıştır.

Şekil 1 Basamak mimarisi (başlangıçtaki hali ve sonradan gizli birimlerin eklenmesini göstermektedir. Dik çizgiler içerideki tüm aktivasyon toplamını gösteriyor. Kutu bağlantılar ise donmuş halde olanlar, X bağlantılar ise tekrarlı eğitimlerdir) (Fahlman ve Lebiere, 1990)

Öğrenme algoritması gizli birimler olmadan başlar. Giriş-çıkış direkt bağlantılarına ilaveten mümkün olan tüm eğitim seti de eğitime tabi tutulur. Gizli birimler boyunca geri yayılım gerekmeksizin, Widrow-Hoff veya ‘delta’ kuralı, Algılayıcı (Perceptron) öğrenme algoritması veya tek katmanlı ağlar için herhangi iyi bilinen öğrenme algoritması kullanılabilir. Tezin içerisinde de basamak korelasyon ağı için yukarıda da bahsedildiği üzere Quickprop algoritması kullanılmıştır. Gizli birimler yokken, quickprop algoritması delta kuralı gibi çalışır, ancak daha hızlı yakınlaşır. Belli bir yerde, bu eğitim bir asimptot’a (asymptote) yaklaşır. Birkaç defa tekrar eden eğitim döngüsünde hata da kayda değer bir azalma meydana gelmediği zaman, hatayı ölçmek için ağ son kez çalıştırılır. Eğer ağın performansı tatmin edici düzeyde ise, döngü durdurulur, eğer değilse, bazı atık hata değeri kalmıştır ileriki safhalarda düşürülmek istenen. Bunu başarabilmek için yeni bir gizli birim ağa eklenir. Net’e yeni birim eklendiğinde, giriş ağırlıkları donar (frozen) ve tüm çıkış ağırlıkları bir kez daha quickprop kullanılarak eğitilir. Bu döngü hata payı kabul edilebilecek şekilde devam eder (veya pes edilinceye kadar) (Fahlman ve Lebiere, 1990).

Fahlman ve Lebiere (1990) tarafından bulunan bu algoritmanın 11 temel adımları aşağıda sunulmuştur:

Adım 1: Problem tarafından verilen tüm giriş ve çıkışlar birbiriyle bağlantılı olacak şekilde başlanır.

Adım 2: Tüm bağlantılar bilinen bir öğrenme algoritması ile eğitilir ta ki karesel hata değeri (Es) anlamlı bir şekilde düşmeyecek şekilde.

(6)

m çıkış sayısını, Np eğitim seti büyüklüğünü, y_i,p sinir ağından i’ninci çıkışı, t_i,p ise ilgili hedefi belirtir.

Adım 3: Tüm ağın dış girişlerinden ve eğer varsa var olan önceki gizli birimlerinden aday bir birim oluşturulur. Bu aday birim henüz aktif olan ağın çıkışına bağlı değildir.

Adım 4: S_c olarak gösterilen (Denklem 7) korelasyonu maksimize edecek şekilde birim (ağırlıkları) eğitilir. Öğrenme, sıradan bir algoritma ile çok fazla zaman alır; korelasyon daha fazla ilerleyemediği zaman eğitim durur ve bunun denklemi ise aşağıda belirtilmiştir;

(7)

z_o,paday gizli birimin çıkışını, E_i,pise adım 2 de hesaplanan (E_i,p=y_i,p-t_i,p) çıkışların artık hata değerini belirtmektedir. Bir niceliğin üstündeki çizgi eğitim seti üzerindeki ortalamayı gösterir.

Adım 5: Aday birimi çıkışlara bağlanır ve giriş değerleri dondurulur. Bu sayede aday birim fazladan giriş birim olarak hareket eder.

Adım 6: Adım 2’de de belirtildiği üzere, giriş-çıkış bağlantıları tekrardan karesel hata değer (Es)’ini minimize edecek şekilde eğitilir.

Adım 7 ve Adım 10: Adım 3’ten Adım 6’ya kadar olan kısmı bir seferde gizli birim ekleyerek tekrar edilir.

Adım 11: E, net hatası verilen bir değerin, ɛ, altına düştüğü zaman eğitim durdurulur. Tek bir aday birim yerine, aday birimlerin olduğu bir havuzdan her biri farklı başlangıç ağırlık kümesi kullanmak daha iyidir. Hepsi aynı giriş sinyallerini alır ve her bir eğitim modeli için aynı artık hata görülür. Çünkü onlar birbirleriyle etkileşime geçmez veya aktif ağı etkilemez, aynı anda eğitilmiş olabilirler. Sadece adaylardan hangisinin korelasyon skoru iyiyse o yüklenir. Aday havuz sistemini kullanımı eğitimi kötü yönde etkileyecek ve onu durdurabilecek bir birimin yüklenmesi riskini ortadan kaldırıyor. Fahlman ve Lebiere (1990), her bir havuzun içerisinde dört veya sekiz aday birimin olma durumunun yeterli olacağını belirtmiştir (Schmitz vd, 2010).

Adım 2 ve Adım 4 rutin bir optimizasyon kullanımı gerektirir. Fahlman bu durum için yukarıda da bahsedildiği üzere Quickprop algoritmasını önermiştir. Quickprop standart geri yayılım algoritması gibi ağırlıklara göre hatanın türevini hesaplar, fakat basit gradyan iniş yerine, quickprop ağırlıkları güncellemek için ikinci derece metodu, Newton’s metoduna göre, kullanır (Fahlman, 1988).

Basamak Korelasyon Sinir Ağı’nın Eğitim Yeterliliği

Eğitimin verimi aday nöronların oluşturduğu havuzda yer değişimi yapılarak geliştirilebilir. Nöronlar ağa girdiğinde hemen öğrenir, ama izole birimler gibi davranırlar, böylece diğerlerinin eğitimini etkilemezler. Sinir yaratım adımının sonunda en iyi olanı aktive edilir, diğerleri sistemden atılır. Çok fazla nöron kullanımı lokal minima’ya takılıp kalmayı ve standart ileri beslemeli geri yayılımlı Yapay Sinir Ağı (YSA)’na nazaran probleme daha uygun sonuçlar verir. Aday nöronlar farklı aktivasyon fonksiyonuna sahip olabilirler böylece homojen olmayan bir ağ kurulabilir ki bu durum daha iyi bir genelleşme yeteneğinin oluşmasını sağlar. Çünkü bu mimaride sadece bireysel nöronlar eğitilir, daha fazla nöronların özellik sezinleyici hedefi değişmez ve hareketli hedef problemi ortadan kalkar. Ayrıca nöronların bireysel eğitimi adım büyüklüğü problemini de kolayca halledilebilmesine olanak verir. Çünkü sadece bir nöron aynı anda odaklanılıp (aday nöronlar izole edilmiştir), sadece bir adım büyüklüğü parametresi ayarlandığında ‘cesurca’ seçilen büyük adımlarla hedefe doğru daha hızlı adım atılır. Hatayı geriye doğru yaydığı ve ağın çıkışı hesaplandığı zaman geri yayılım algoritması bir ileri ve bir geri yayılması gerekir. Bu durumun tersine ağın çıkışını hesaplamak ve bu bilgiyi aday nöronlarda eğitim amaçlı kullanmak için basamak korelasyon ağı sadece bir ileri yayılması gerekir. Çünkü adaylar aktif ağı üzerinde herhangi bir etkisi yoktur, eğitim zamanı depolama ve eğer yeteri kadar hafıza var ise tüm eğitim örnekleri için ağın çıkışlarının tekrar kullanımı durumları için azaltılabilir. Başlangıç anında veya aday nöronun aktifleştirilme sonrası basit bir gradyan iniş algoritması ağın bağlantılarının çıkışlarını eğitmek için kullanılabilir (Bal´azs, 2009).

Basamak korelasyon sinir ağı herhangi bir eğitim setini temsil etmekte çok anlamlı bir güce sahip, ama bir durum söz konusu o da kolayca aşırı uyum (overfit)’lu bir hale gelebilir. Bu durumu kontrol etmek için izole edilmiş eğitim setleri validasyon seti veya adaptif model seçim tekniği olarak Schuurmans ve Southey (2002) tarafından sunulmuştur.

Basamak Korelasyon Sinir Ağının Derinliğinin Azaltılması

Her bir aday nöronun yeni bir katmana gitmesinden dolayı, Basamak Korelasyon Sinir Ağı eğitimi yavaş veri çıktı yetenekleriyle- ki bu verimsiz ağ çıkış hesaplanmasına yol açar, derin ağlar üretir. Bu derinlik Baluja ve Fahlman (1994) tarafından yayımlanan makalesinde de gösterildiği üzere basit bir basamak korelasyon sinir ağı çeşidi olan kardeş/soyundan (sibling/descendant) basamak korelasyon sinir ağı (KSBKSA) ile azaltılabilir (Baluja ve Fahlman, 1994). Yeni geliştirilen bu ağda çeşitli aday nöronlar havuzu iki parçaya bölünür ve bunlara kardeş ve soyundan birimler diye isimlendirilir. Soyundan birimler basamak korelasyon sinir ağının tipik eğitim ağında bağlanırlar, kardeş nöronlar ise son katmanın nöronlarına değil bir öncekinin nöronlarına bağlanırlar. Kardeş ve soyundan birimler öğrenme süreci boyunca her biri birbirleriyle yarış halindedirler, sadece bir tanesi aktif edilmek için seçilir. Eğer kardeş birim seçilirse, geçerli olan ağın son katmanına koyulur. Soyundan bir nöron durumunda basamak korelasyon sinir ağı eğitim zamanında yapıldığı gibi yeni bir katman yaratılır. Kardeş birim asla aktive edilmez, çünkü daha az bağlantılara sahiptir ve ayrıca soyundan bir nöron gibi iyi bir özellik sezinleyici olamaz. Fakat bazı durumlar bu yargıyı anlamsız kılar. Eğer ek bağlantılar soyundan birime anlamlı bir bilgi sağlamazsa, öğrenme algoritması ilgili ağlar sıfıra yakın değişir. Eğer bu durum oluşursa, kardeş birimler daha hızlı yakınsar ve aday eğitim sürecinin sonunda daha iyi sonuçlar sağlar ve böylece soyundan birim yerine kardeş birim aktive olur (Bal´azs, 2009).